2018-10-06

標準化と中心化

Pythonで標準化とか中心化はどうやってやるんだろうという話です．

結論だけ書きます．（そのうち合間を見て加筆します）

このページではこういうデータを使います
f:id:shu10038:20181006173233j:plain

標準化

from scipy import stats
x = df.iloc[:, 2:6].apply(stats.zscore, axis=0)
x.head()

f:id:shu10038:20181006173231j:plain

標準化されているかを調べます
f:id:shu10038:20181006173229j:plain
平均ほぼ0，分散(標準偏差)ほぼ1

中心化

y = df.iloc[:, 1].apply(lambda v:v-df.iloc[:, 0].mean() ).astype(float)
y.head()

2018-09-08

バイアス-バリアンス分解の導出を真面目にやる

数理統計学

どうもです．

只今，下記の書籍にを用いて勉強中です．

応用をめざす数理統計学 (統計解析スタンダード)

作者: 国友直人
出版社/メーカー: 朝倉書店
発売日: 2015/08/25
メディア: 単行本（ソフトカバー）
この商品を含むブログを見る

P118のあたりに推定の偏りの話や，不偏推定量の事が述べられています．そして推定量の真の母数と推定量の二乗誤差の期待値を計算する所では次の式が書いてありました．

f:id:shu10038:20180920215318j:plain
さぁ，なんということでしょう～，式の行間が開きすぎてよくわかりません．他の書籍で調べてもこんな感じで端折ってありますし，ネットで調べても「期待値の計算すれば上手いこと消えてほしい項が0になってくれます」みたいな感じで，きちんとと書いている記事が直ぐには見当たりませんでした．
なので，折角なので勉強がてらに式の展開をしてみます

展開

二乗誤差を計算すると

f:id:shu10038:20180920215319j:plain
ここで，第三項について， $\theta$ と $E\left( \hat { \theta } _{n} \right)$ は定数であることを考慮すると，
f:id:shu10038:20180920215320j:plain
よって，元の式は
f:id:shu10038:20180920220322j:plain

2018-08-08

Windows環境下でPython版のglmnetを使うとどうなるか？

夏のある日のこと，
私はLasso回帰を用いてあるデータを分析しようとしていた．

glmnetを呼び出して実行したところ，

x input must be a scipy float64 ndarray

とエラーメッセージが帰ってきた．

あれ？っと思ったけど，その日に扱っていたのは整数値だったことを思い出した．
しゃぁ無いから浮動小数点数にキャストしてみたんだ．
これで間違いは無いはず．
スクリプトを実行してみると・・・

raise ValueError('loadGlmlib does not currently work for windows')
ValueError: loadGlmlib does not currently work for windows

なん・・・だと・・・・
これwindows環境では動かんのかい！！
諦めて，教えてもらったAzureNotebookを使うかな．

参考

2018-07-13

StatsModelsとscikit-learnのElastic Net(Lasso回帰)を比較してみた

Python3.X スパース推定コラム多変量解析

　最近スパース推定の勉強会に参加しております．使っているテキストはこちら．

スパース推定法による統計モデリング (統計学One Point)

作者: 川野秀一,松井秀俊,廣瀬慧
出版社/メーカー: 共立出版
発売日: 2018/03/08
メディア: 単行本
この商品を含むブログを見る

この本の第２章のElastic Netについて勉強がてらにプログラムを書いてみて，振る舞いを観察してみました．

　今回使うデータはこちら．リンク先のヘッダの「Earn」が観測日の売上．「MaxTemp」が観測日の最高気温で「MinTemp」が最低気温．「Humi」は観測日の湿度．「Wind」は風の強さ．「Sun」は日照時間です．この「Earn」売上に直結する項目は何かを分析することが目的です．
ちなみに，このデータは昔お世話になったアイスクリーム屋さん・ハンバーガ屋さんの統計をイメージして作成したものです．なので実際の現象とは異なりますのであしからず．

各項目の相関係数を出してみるとこんな感じです．「Wind」がわざとらしいほどに無相関ですね．
f:id:shu10038:20180713095238p:plain
各項目の関係をグラフにするとこんな感じ．
f:id:shu10038:20180712223511j:plain
明らかに「Wind」がやる気がない数字が入ってますね．（まぁ，だってそういう風に作ったんだもん）

StatsModelsのエラスティックネットを用いてPython スクリプトを書いてみた

　統計を用いた分析をする時に「StatsModels」を使うか「scikit-learn」を使うか悩ましかったりします．StatsModelsはPandasのDataFrameを直接使うことができるので，私はどちらかというとStatsModelsを使うことが多いですね．現時点ではscikit-learnはDataFrameを受け付けないですが，そのうち変更があったらどうなるか分かりません．といってもscikit-learn昔書いたこちらの記事を参照にDataFrameからListに変換してあげればいいだけなんですけどね．

StatsModelsのエラスティックネットのドキュメントはこちらこちら

さて，下記のように書いてみました．

この書籍では罰則項を増加させたときの回帰係数を描画した解パス図というのを紹介していました．これに習って同じものを描いてみるとこんな感じ．
f:id:shu10038:20180714090330j:plain
あれ？なんか変だぞ？？この場合は一番売上に一番関係なさそうな「Wind」が先に消えるんじゃないの？？
なんか変なのでscikit-learnではどういう振る舞いを見せるのかやってみました．

scikit-learnによるエラスティックネット

scikit-learnを使ったエラスティックネットはネット上にサンプルコードが山ほどあるのでここでは特に記載しません．Gitには上げておいたので，興味がある方は下記を参照ください．

Jupyter Notebook Viewer

さて，同じように解パス図を書くとこんな感じ．
f:id:shu10038:20180714090331p:plain

あれ？StatsModelsとsklearnで結果が違う・・・・
そんな馬鹿な，，という感じですが原因不明です．これでは余りにも内容がない記事になってしまいますので，あとで加筆します．

ではそんな感じで．ではでは．

2018-06-10

データフレームの各行の差を計算してグラフ化する：Pandas

Pandas Python3.X 小技メモ

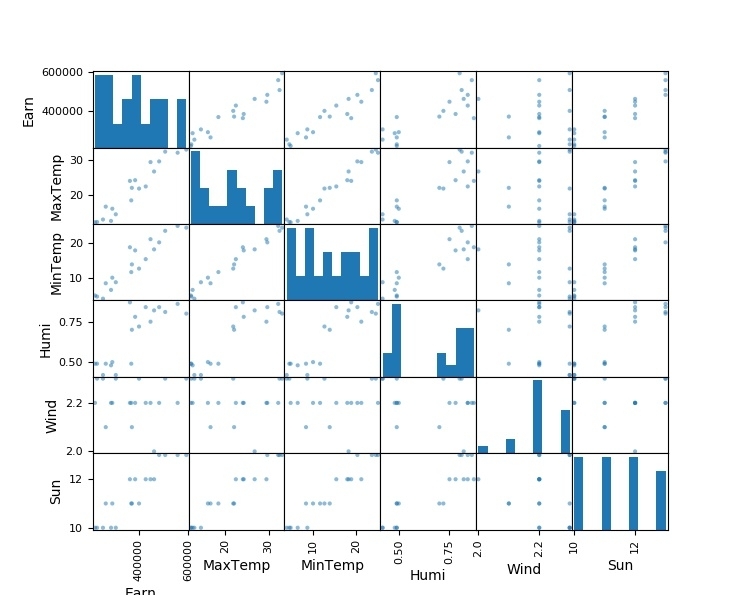
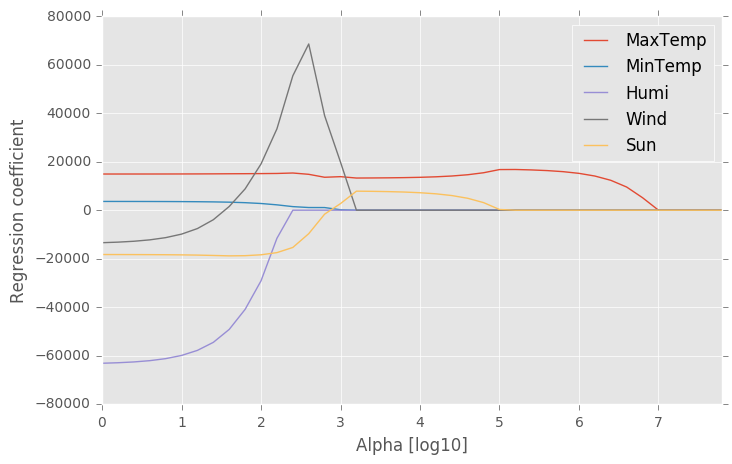
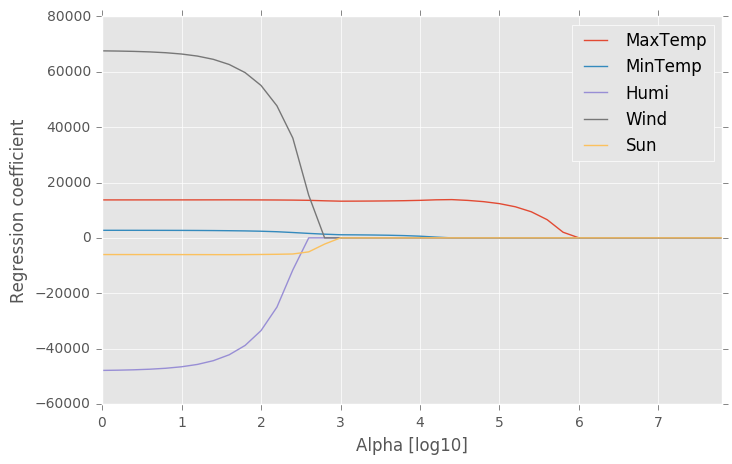
やりたいことしては，タイトル通り『データフレームの各行の差を計算してグラフ化する』ことです．Pandasのデータフレームを用いて各列の時間差を計算してグラフに出力するということをやります．

今回はTimedelta型を使っているのですが，データフレームの差を計算して描画しようとすると「'Timedelta' object has no attribute 'plot'」というエラーメッセージ出てきます．無理やりint型になおして出力するとナノ秒になってしまうので，これを上手く工夫して出力しなくてはなりません．

ここからが本題

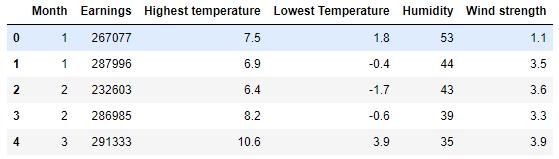
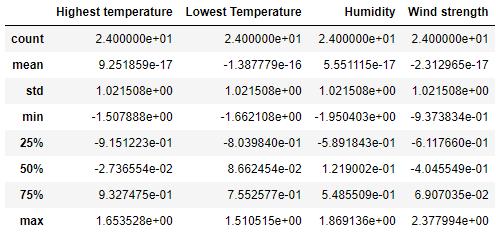
さて，こんなデータを使います．各駅の名前とそこを通過する時間が記載されているデータがあるとします．

//time.csv
hakata,10:00:05.156
yoshiduka,10:29:54.731
kadomatu,11:03:44.195
katuragawa,11:38:32.395
tendou,12:09:21.151
iiduka,12:46:10.364
kokura,13:21:59.996

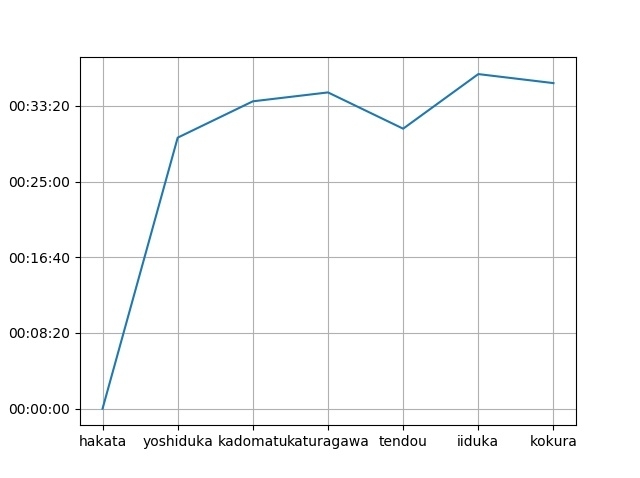
このとき前の駅から今の駅まで到着するのにかかった時間を計算してグラフに出力します．

Python3のコード

import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.mlab as mlab

# CSVデータの読み込み
df = pd.read_csv('data/time.csv', header=None, names=['sta', 'time'])

# 時間型に変換
df['time'] = df['time'].apply(lambda xx: pd.to_datetime(xx))

# 時間差の計算．各行の差を計算する
df_e =df['time'].diff(1).fillna(0)

# 描画
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(df['sta'], df_e)

# ナノ秒から変換
def toChange(y, i):
    h = int(y / 1000000000 / 3600)
    m = int(y / 1000000000 / 60)
    s = int(y / 1000000000 % 60)
    return '%(h)02d:%(m)02d:%(s)02d' % {'h': h, 'm': m, 's': s}

from matplotlib.ticker import FuncFormatter as ff

ax.yaxis.set_major_formatter(ff(toChange))
plt.grid()

plt.show()

結果

するとこんなふうに出力されます
f:id:shu10038:20180610204723j:plain

2018-05-27

Pandasデータフレーム内の複数の文字を「.str.split」を使って区切る

小技メモ Python3.X Pandas

Pandas(＠Python)のデータフレーム内のstringを複数の文字で区切りたい場合があります．
「.str.split」を使うのですが少し工夫が必要です．
まぁ，簡単に言うと縦棒「|」で区切るわけですよ．

import pandas as pd
df = pd.DataFrame(
        {'Time': ['jt=10:00:00:-p', 'jt=10:01:01:-p', 'jt=10:10:02:-p', 'jt=10:50:03:-p', 'jt=11:00:04:-p'],
           'Value': [25, 30, 104, 52, 41]})

df_spr = df['Time'].str.split('=|:-', expand=True)

print(df_spr)

出力すると・・

    0         1  2
0  jt  10:00:00  p
1  jt  10:01:01  p
2  jt  10:10:02  p
3  jt  10:50:03  p
4  jt  11:00:04  p

2018-04-15

ベイズ更新をやってみた！

Python3.X ベイズ統計コラム

３月の末にベイズ推定の勉強会に参加してきました！
math-unknown.connpass.com
この勉強会では単に講師の話を聞くだけではなく，みんなでワイワイディスカッションしながら進めるような形式で，グループ内の誰かが疑問に思ったことを後で調べることでより理解が深まったように思います．
そして講師の方の説明の流暢さに脱帽でした！

その中でもベイズ更新の例としてオオカミ少年の例が興味深いと思いました．勉強会の案内のところに次のリンクが貼ってあったので，共有しておきます．
okandayo.hatenablog.com
ベイズ更新を使ってオオカミ少年の例をシミュレーションしてみようと思いましたが，なかなか時間がなく出来ませんでした．ようやく取り掛かることが出来たのでちょこっとやってみたわけです．

問題設定

次のような風に問題文を作ってみます．「オオカミ少年」のお話は昔NHKの番組で見たことがある程度なのでうろ覚えですが，少年が嘘をついて「オオカミが来たぞ！」と叫んでいるうちに村人が誰も少年を信用しなくなってしまい，本当にオオカミが来た時に村人が食べられてしまった話だったと思います．

問題文；オオカミ少年
ある村では嘘つきは75%の確率で嘘をつき，正直者は85%の確率で本当のことを証言することが知られている．
この村のある少年は事あるごとに「オオカミが来たぞ！」と叫んでいるが，本当に狼が来るときと来ない時があるようだ．この少年は嘘をついている，もしくは時々間違えるようである．この少年が100回叫んだ結果から，この少年は正直者か嘘つきかを答えよ．

問題文から仮定と各値を書き出す

この問題文から，次の様のような仮定を置きます．

$H_{1}$ ：少年は嘘つき
$H_{2}$ ：少年は正直者

「オオカミが来たぞ！」と叫ぶイベントに対して，本当にオオカミが来る事象と来ない事象があります．これを次のように置きます．

$A$ ：少年は嘘をつく（「オオカミが来たぞ！」と叫んだときにオオカミが来ない）
$\bar { A }$ ：少年は本当のことを言う（「オオカミが来たぞ！」と叫んだときにオオカミが来る）

$A$ と $\bar { A }$ は「オオカミが来たぞ！」と叫んで来ないときと実際に来たときに相当します．これらには次の図のような関係があります．
]

さて，次に問題文からそれぞれの値を次のように置きます．

：ある村で嘘つきが本当の証言をする確率
- →嘘つきが「オオカミが来たぞ！」と叫んで，オオカミが来る確率
：ある村で正直者が本当の証言をつく確率
- →正直者が「オオカミが来たぞ！」と叫んでオオカミが来る確率
：ある村で嘘つきが嘘の証言をする確率
- →嘘つきが「オオカミが来たぞ！」と叫んでもオオカミが来ない確率
：ある村で正直な人が間違えて嘘の証言をする確率
- →正直者が間違えて「オオカミが来たぞ！」と叫んでオオカミが来ない確率

これを表にするとこんな感じです．

	オオカミが来る $A$	オオカミが来ない　 $\bar { A }$
嘘つき $H_{1}$	0.15	0.85
正直　 $H_{2}$	0.75	0.25

更新則を求める

さて，次にベイズの定理と全確率の公式から

「オオカミが来たぞ！」と叫んで本当に狼が来た場合，少年が嘘つきである確率
「オオカミが来たぞ！」と叫んで狼が来なかった場合，少年が嘘つきである確率

をそれぞれ求めます．ベイズの定理と全確率は下記を参照ください．

「オオカミが来たぞ！」と叫んで本当に狼が来た場合，少年が嘘つきである確率

$\begin{eqnarray*} P\left( { H_{ 1 } }|{ A } \right) & = & \frac { P\left( { A }|{ H_{ 1 } } \right) P\left( { H_{ 1 } } \right) }{ P\left( { A } \right) } \\ & = & \frac { P\left( { A }|{ H_{ 1 } } \right) P\left( { H_{ 1 } } \right) }{ \sum _{ H }^{ }{ P\left( { A }|{ H } \right) P\left( { H } \right) } } \\ & = & \frac { P\left( { A }|{ H_{ 1 } } \right) P\left( { H_{ 1 } } \right) }{ P\left( { A }|{ H_{ 1 } } \right) P\left( { H_{ 1 } } \right) +P\left( { A }|{ H_{ 2 } } \right) P\left( { H_{ 2 } } \right) } \end{eqnarray*}$

「オオカミが来たぞ！」と叫んで狼が来なかった場合，少年が嘘つきである確率

$\begin{eqnarray*} P({ H_{ 2 } }|\overline { A } ) & = & \frac { P({ { \overline { A } } }|{ H_{ 2 } })P\left( { H_{ 2 } } \right) }{ P({ { \overline { A } } }) } \\ & = & \frac { P({ { \overline { A } } }|{ H_{ 2 } })P({ H_{ 2 } }) }{ \sum _{ H }^{ }{ P({ { \overline { A } } }|{ H })P\left( { H } \right) } } \\ & = & \frac { P({ { \overline { A } } }|{ H_{ 2 } })P\left( { H_{ 2 } } \right) }{ P({ { \overline { A } } }|{ H_{ 1 } })P\left( { H_{ 1 } } \right) +P({ { \overline { A } } }|{ H_{ 2 } })P\left( { H_{ 2 } } \right) } \end{eqnarray*}$

シミュレーション

次に実際にシミュレーションしてみます．Pythonでこんな感じに書きました．

import numpy as np
import matplotlib.pyplot as plt

# 確率の設定
p_AH1 = 0.15 # 嘘つきがが嘘をついてオオカミが来ない確率
p_AH2 = 0.75 # 正直者が本当のことを言ってオオカミが来る確率
p_barAH1 = 0.85 # 嘘つきが間違えて正しいことを言う確率
p_barAH2 = 0.25 # 正直者が間違える確率

# 嘘つきである確率の初期値
p_l = [0.5]

# ループ計算
for i in range(99):
    rand = np.random.random()

    #「オオカミが来たぞ！」と叫んだときに狼が来る
    if rand >0.5:
        p_l.append(p_l[i]*p_barAH1/(p_barAH1*p_l[i]+p_barAH2*(1-p_l[i])))

    #「オオカミが来たぞ！」と叫んだときに狼が来ない
    else:
        p_l.append(p_l[i]*p_AH1/(p_AH1*p_l[i]+p_AH2*(1-p_l[i])))

# 描画        
plt.plot(range(100),p_l)
plt.xlabel('times')
plt.ylabel('H1')
plt.grid()
plt.show()

シミュレーション結果

狼が来る確率を0.4．0.5，0.6とそれぞれ変化させてみたのが下の図です．（ちなみにx軸のレンジが100だと見づらいので80にしています）

今回は問題設定上，正直者と判定されやすいのでこうなりました．
ただし，狼が来る確率を0.4の場合には毎回結果が異なり，正直者と判定される場合や嘘つきと判定される場合に分かれました．その様子を表したのが下の図です．

というわけで今日はこんな感じで．

標準化

中心化

展開

参考

StatsModelsのエラスティックネットを用いてPythonスクリプトを書いてみた