ポアソン分布とガンマ分布から事後分布を導出して，事後期待値や予測分布などを求める

この前までとある所で一般化線形モデルから始まるベイズモデリングの勉強に参加していました．一般化線形モデルを通して勉強したのは初めてかもしれません．ということでベイズモデリングについて体系的に勉強するために記事を書いてみようと思います．

この記事ではまず手始めとしてある例題をもとに，ベイズの定理を用いて事後分布を導出する過程について述べます．

こんな例題を考えてみる

この記事では割とよくある例題として，次のような観測値がポアソン分布，事前分布をガンマ分布という場合を考えてみます．

例題
ポアソン分布に従う５つの観測値[2 ,3 ,0 ,4 ,1]が得られたとする．またこのポアソン分布のパラメータは $\alpha=15，\beta=2$ のガンマ分布とする．このとき，

事後期待値

事後分散

予測分布

を求める

得られる標本がポアソン分布に従うものとし，共役な事前分布としてガンマ分布を選んだときに事後分布もガンマ分布になる例を示します．

まず事前分布を決める

問題にあるように事前分布としてガンマ分布を考えます．ガンマ分布の密度関数は次のように与えられます．

$\begin{aligned} f(x|\alpha, \beta )=\frac{\beta ^ \alpha }{ \Gamma (\alpha) }x^{\alpha-1}e^{-\beta x } \end{aligned}$

\alpha=15，β=2を与えた場合は次のようになります．
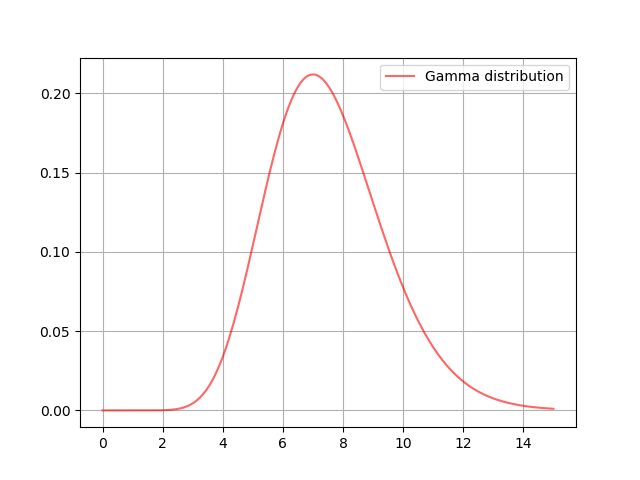
f:id:shu10038:20191222191203p:plain

観測値から尤度関数を求める

観測値[2 ,3 ,0 ,4 ,1]が与えられた場合は尤度関数は次のように与えられます．

$f(x|\theta )= \prod_{i=1}^n \frac{\theta ^{x_i} \exp(- \theta ) }{x_i! }$

事前分布と尤度関数を合わせて描画すると次のようになります．
f:id:shu10038:20191222191155p:plain

事前分布と尤度関数から事後分布を求める

事後分布は次のようになります．

$\begin{eqnarray*}f(\theta|x )&=& \frac{ f(x \mid \theta ) f( \theta )}{ f(x) } \\ &\propto& \prod_{i=1}^n \frac{\theta ^{x_i} \exp(- \theta ) }{x_i! }\frac{\beta ^ \alpha }{ \Gamma (\alpha) }\theta^{\alpha-1}e^{-\beta \theta } \\ &\propto & \theta ^{ \alpha + \sum_{i=1}^{n} x_{i} -1 } e^{- n \theta -\theta \beta} \end{eqnarray*}$

このように定数以外はガンマ分布同じ形状になりました．パラメータも次のように更新されます．

$\begin{eqnarray*}\alpha' &=&\alpha + \sum_{i=1}^{n} x_{i}=25\\ \beta'&=& n + \beta=7 \end{eqnarray*}$

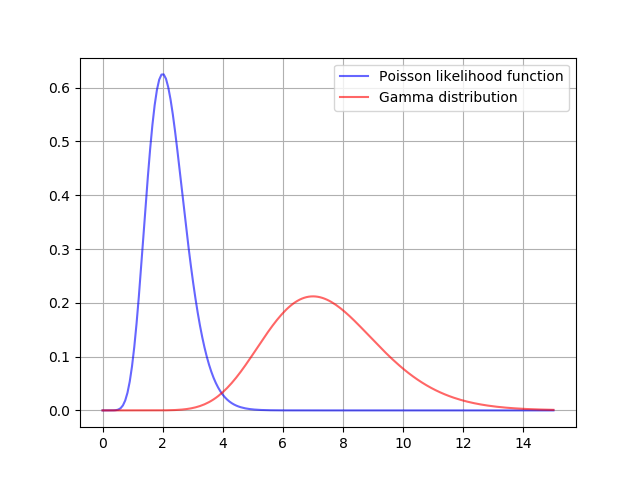
事前分布と尤度関数と合わせて描画すると次のようになります．観測値をもとに，事前分布が更新されています．
f:id:shu10038:20191222191158p:plain

事後分布から事後期待値，事後分散，予測分布をもとめる

事後分布がガンマ分布になることが分かったので，ガンマ分布の期待値と分散の計算より，

$\begin{eqnarray*} E( \theta \mid x) &=& \alpha' \beta' = 175\\ V( \theta \mid x) &=& \alpha' \beta'^{2} = 1225 \end{eqnarray*}$

予測分布は次のとおりです．

$\begin{eqnarray*} f(x^*|x ) &=& \int_0^ \infty { f(x^* \mid \theta ) f( \theta\mid x )} d \theta \\ &=& \int_0^ \infty \frac{\theta ^{x_i} \exp(- \theta ) }{x_i! }\frac{\beta ^ \alpha }{ \Gamma (\alpha) }\theta^{\alpha-1}e^{-\beta \theta }d \theta \\ &=& \frac{\beta^\alpha}{x^*!~ \Gamma (\alpha)} \int_0^ \infty \theta^{x^* +\alpha -1} e^{-\theta(1+\beta) }d \theta ~~~~~~ \ldots (1) \\ \end{eqnarray*}$

ここで ${\theta(1+\beta)=k }$ とおくと， ${\frac{d \theta}{dk}=\frac{1}{1+\beta} }$ なので

$\begin{eqnarray*} 式(1)&=&\frac{\beta^\alpha}{x^* !~ \Gamma (\alpha)} \int_0^ \infty \left(\frac{1}{1+\beta}\right)^{x^* +\alpha -1} e^{-\theta(1+\beta) } \frac{1}{1+\beta} dk \\ &=&\frac{\beta^\alpha}{x^*!~ \Gamma (\alpha)} \left(\frac{1}{1+\beta}\right)^{x^*+ \alpha }\int_0^ \infty k^{x^* +\alpha -1} e^{- k}dk ~~~~~~ \ldots (2) \\ \end{eqnarray*}$

上式について，ガンマ関数の定義より，

$\begin{eqnarray*} \int_0^ \infty k^{x^* +\alpha -1} e^{- k}dk = \Gamma (x^* +\alpha) \end{eqnarray*}$

であり，またガンマ関数の性質より

$\begin{eqnarray*} x^*!= \Gamma (x^* +1) \end{eqnarray*}$

なので，

$\begin{eqnarray*} 式(2)&=&\frac{ \Gamma (x^* +\alpha)}{ \Gamma (x^*+1) \Gamma (\alpha)} \beta ^ \alpha (1+ \beta )^{-(x^*+ \alpha )} ~~~~~~ \ldots (3) \end{eqnarray*}$

ここで，

$\begin{eqnarray*} \beta = \frac{1-p}{p} \end{eqnarray*}$

とおくと，

$\begin{eqnarray*} 式(3)&=&\frac{ \Gamma (x^* +\alpha)}{ \Gamma (x^*+1) \Gamma (\alpha)} \left(\frac{1-p}{p}\right) ^ \alpha \left( 1+ \frac{1-p}{p} \right)^{-(x^*+ \alpha )}\\ &=&\frac{ \Gamma (x^* +\alpha)}{ \Gamma (x^*+1) \Gamma (\alpha)} \left(\frac{1-p}{p}\right) ^ \alpha \left( \frac{1}{p} \right)^{-(x^*+ \alpha )}\\ &=&\frac{ \Gamma (x^* +\alpha)}{ \Gamma (x^*+1) \Gamma (\alpha)} p^{x^*} \left(1-p\right) ^ \alpha \end{eqnarray*}$