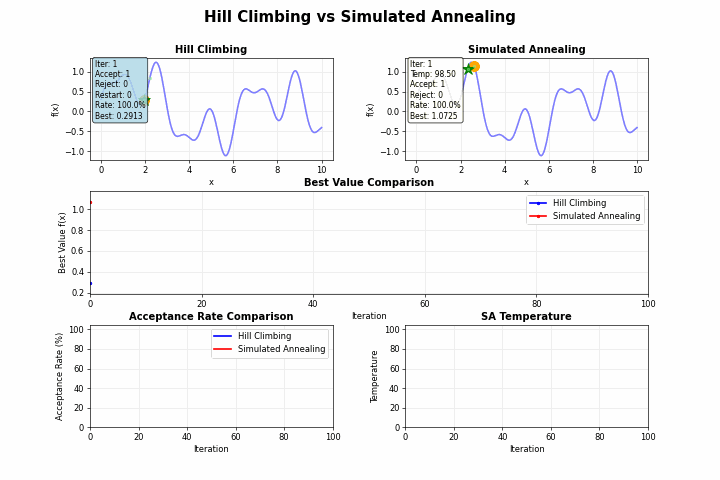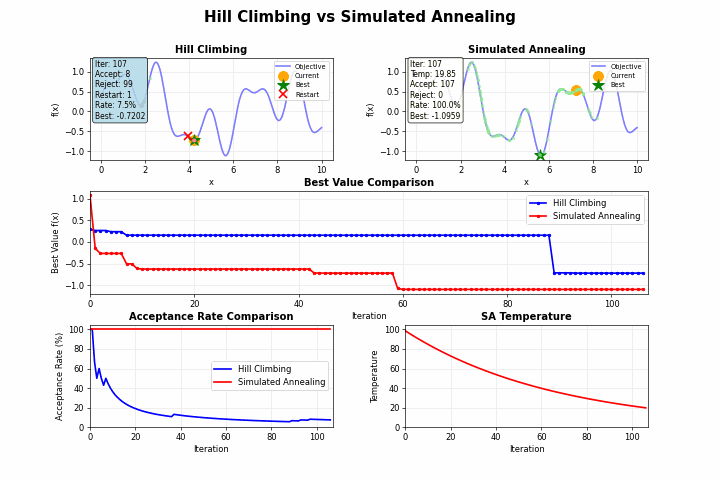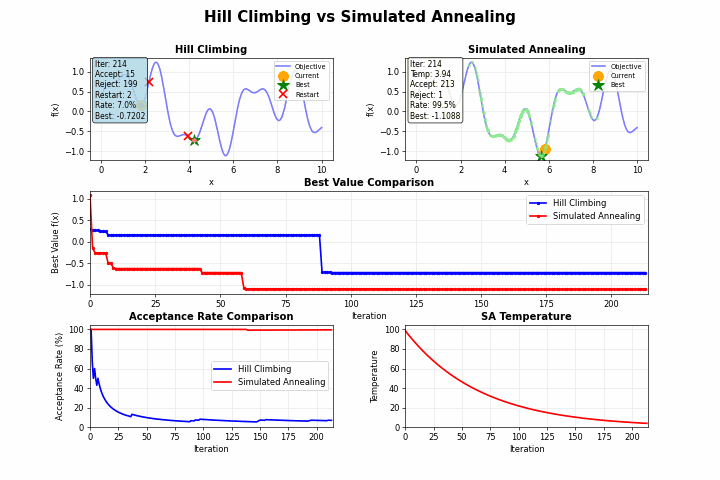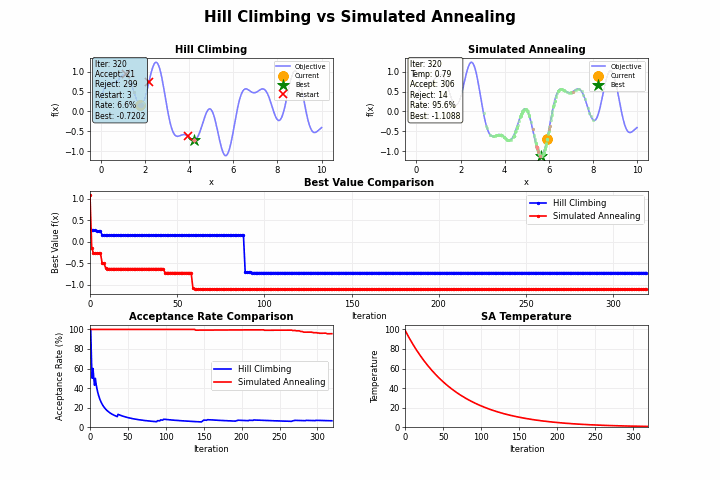
先日、Kaggleのコンペに参加しました。もみの木の形をした樹木を敷き詰めるという問題で、入賞者の多くは焼きなまし法を採用していました。
shu10038.weblog.to
私も昔山登り法や焼きなまし法というのを聞いたことがあるのですが、自分で実装したりしたのは初めてでした。なので勉強がてらにこの記事を作成しました。
焼きなまし法とは
最適化問題に取り組んだことのあるならば、一度は「局所最適解」という言葉を耳にしたことがあるかと思います。昔は「ローカルミニマム」という言い方で習った気がします。
山登り法(Hill Climbing)のような単純な探索アルゴリズムは、目の前の改善のみを追求するあまり、より良い解が他にあるにもかかわらず、早期に探索を終了してしまうことがあります。
しかし、焼きなまし法を用いることで、局所最適解から抜け出すこともあります。金属加工における「焼きなまし(アニーリング)」という工程では、金属を加熱してからゆっくり冷却することで、結晶構造の欠陥を減らし、より安定した状態を得ることができます。この物理現象を模倣したのが「焼きなまし法(Simulated Annealing)」です。
焼きなまし法の核心
焼きなまし法の最も革新的な点は、一時的に悪化する移動も確率的に許容するという点にあります。この許容度を制御するパラメータが「温度」です。
温度の計算は単純で、下記のように指数減衰する関数を用います。
# 受理確率の計算式 def acceptance_probability(delta, temperature): if delta < 0: return 1.0 # 改善する場合は常に受理 else: return math.exp(-delta / temperature) # 悪化する場合は確率的に受理
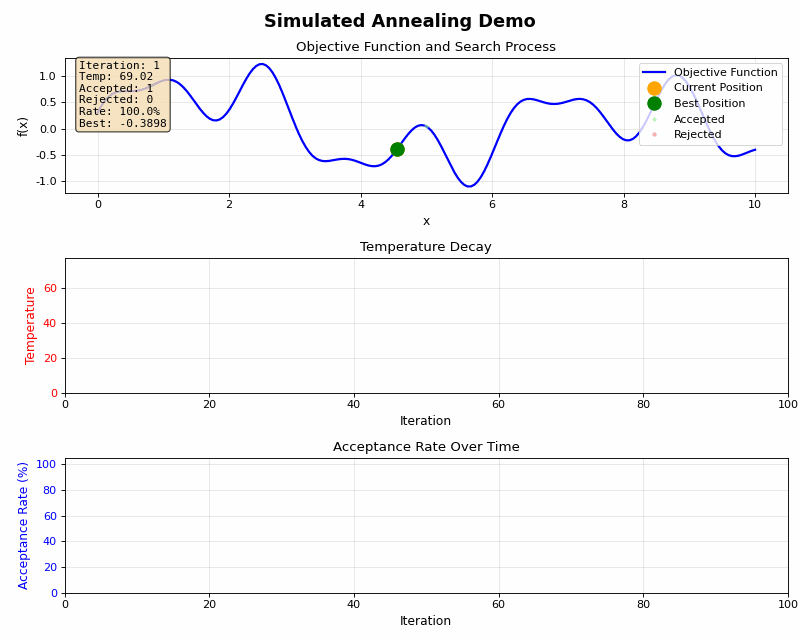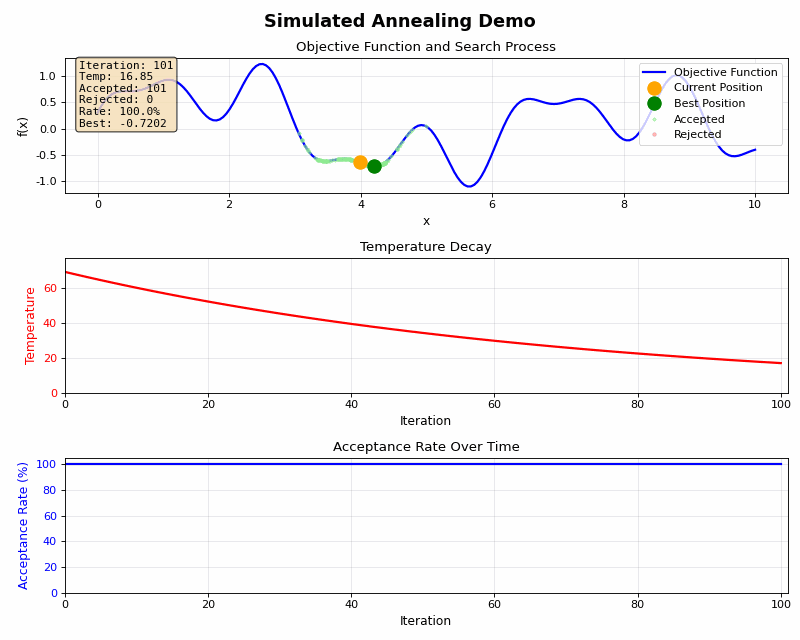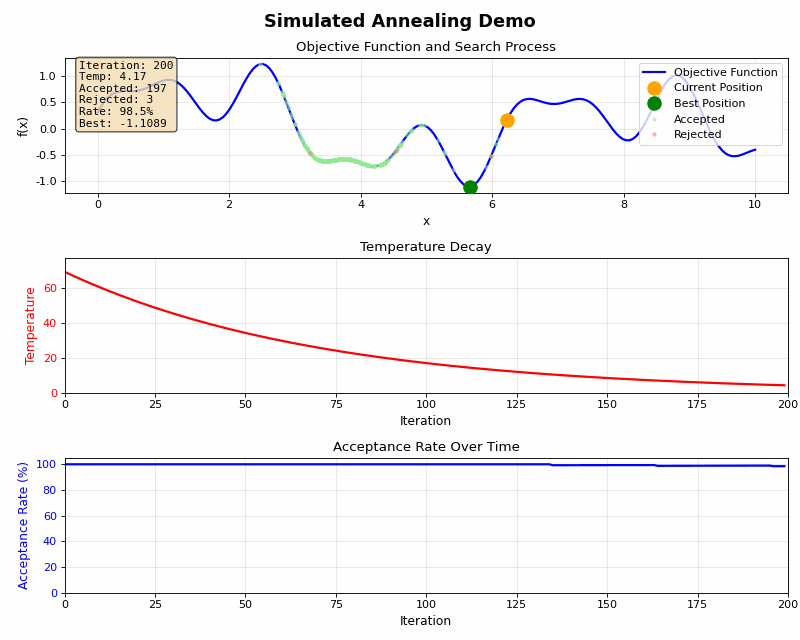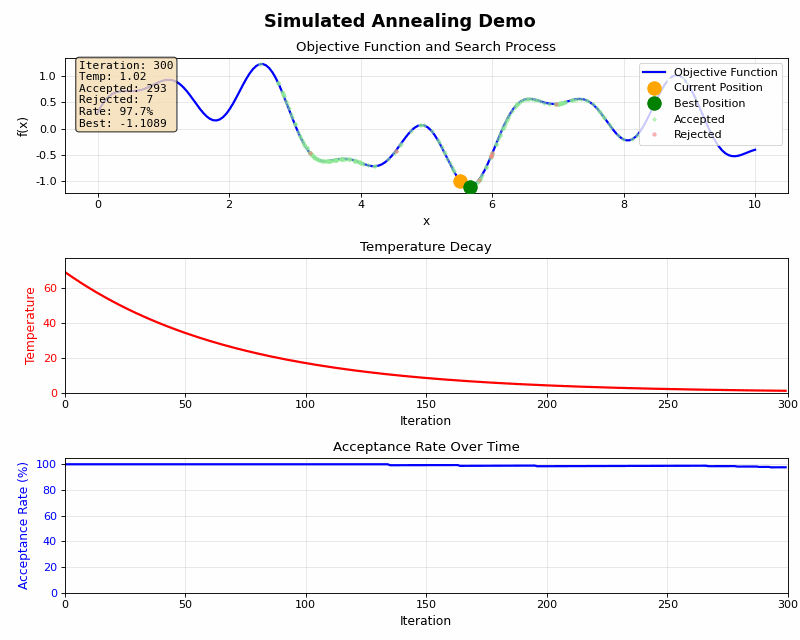
高温時と低温時にはそれぞれ下記のような特徴があります。
高温時(初期段階):
- 温度が高い → exp(-Δ/T) の値が大きい
- 大きな悪化でも高い確率で受理
- 探索モード:広範囲を探索し、局所最適解から脱出
低温時(後期段階):
- 温度が低い → exp(-Δ/T) の値が小さい
- 小さな悪化でもほとんど受理されない
- 活用モード:現在の最適解付近を細かく調整
また温度をゆっくり下げたり、急激に下げたりすることで下記のような特徴があります。
急冷(冷却率が高い):
- 計算時間は短いが、局所最適解に収束するリスクが高い
- 例:冷却率0.9
徐冷(冷却率が低い):
- 大域的最適解を見つける可能性が高いが、計算時間が長い
- 例:冷却率0.99~0.999
温度が可能にするパラダイムシフト
ここで焼きなまし法の真価が発揮されます。高い温度では、「悪化する移動も受け入れる」 ことができます。これが何をもたらすかというと:
「今の整然とした配置を、あえて崩す権利」 です。
# 構造転換のイメージ def structural_change(current_layout): # 高温時:あえて良い配置を崩す if temperature > 50: # 1. 現在:4列に整然と並んでいる # 2. 崩す:あえてランダムに散らす(一時的にスコア悪化) # 3. 再構築:5列に並び替える(最終的にスコア改善) return destroy_and_rebuild(current_layout)
焼きなまし法なし:
■ ■ ■ ■ ← 4列(固定) ■ ■ ■ ■ ■ ■ ■ ■
text
焼きなまし法あり:
初期:■ ■ ■ ■ ← 4列(良いが最適ではない)
高温時:■ ■ ← 一度バラバラに(一時悪化)
■ ■
■ ■
低温時:■ ■ ■ ■ ■ ← 5列に再配置(最終改善)
■ ■ ■ ■ ■
この「一旦崩してから再構築」こそが、焼きなまし法の核心です。