Gitのアクセストークン
結構面倒で,ちょっとハマってしまいました...
【git】パスワードを受け付けなくなりアクセストークンを取得後に行った設定
docs.github.com
Google ColaboratoryでNotebookをHTMLに変換する
Google Colaboratoryはどこでも同じ環境で作業ができるので便利ですが,jupyter labにあるようなHTMLダウンロードの機能がないようです.
そこで下記を参考にしました.
qiita.com
ただ,ファイルの場所を聞かれたりとそのまま使うことが出来なかったので,すこし書き換えました.
何度も書き換えるのが面倒なので,このブログに書き下して,コピペして使えるようにします.
from google.colab import files import re import shutil # そのままHTML化すると上書きされてしまうので,一旦コピーする dir = '/content/drive/MyDrive/・・・コピーしたいファイルが格納されているディレクトリ・・・/' file_name = '・・・今使っているファイルの名前・・・.ipynb' fn = dir+'・・・コピー後の名前・・・.ipynb' shutil.copyfile(dir+file_name , fn) # HTML化 fn_s = re.escape(fn) output_fn = fn.split('.', 1)[0]+'.html' output_fn_s = re.escape(output_fn) !jupyter nbconvert --to html $fn_s files.download(output_fn) !rm $fn_s
Pythonでよく使うコード:その1
忘れて何度も引き直すのでメモ.都度更新予定.
下記に描画編を作りました。
publicjournal.hatenablog.com
publicjournal.hatenablog.com
Pythonの基礎的な操作
qiita.com
qiita.com
9cubed.info
https://www.affrc.maff.go.jp/tsukuba/top/event/workshop/attach/pdf/209ws-12.pdfwww.affrc.maff.go.jp
https://www.affrc.maff.go.jp/tsukuba/top/event/workshop/attach/pdf/209ws-12.pdf:titlessss
qiita.com
リスト内包表記
qiita.com
qiita.com
note.nkmk.me
note.nkmk.me
高速化向き↓
qiita.com
dsas.blog.klab.org
ファイル獲得(glob)
print文関係
その他テクニック
関数名や変数名を付けるときに大文字なのか小文字なのか、アンダーバー使うのか、色々訳分からーん!!
— みやさかしんや@Python/AI/DX (@miyashin_prg) 2022年4月7日
という方のために命名規則をまとめました🌟😀 pic.twitter.com/W5bybLC514
普段、よく使う print()。
— みやさかしんや@Python/AI/DX (@miyashin_prg) 2022年4月7日
意外と知らない便利な使い方がありますのでご紹介します☺ pic.twitter.com/15m9rgE7QL
From:
github.com
PYMC3を実行してみるとエラーが出る
いつもはJupyterからPyMC3を呼び出していましたが,今回はスクリプトを実行してみたところ,次のようなエラーが出たという.
In Windows OS, this usually means that the child process raised an exception while it was being spawned, before it was setup to communicate to the main process.
The exceptions raised by the child process while spawning cannot be caught or handled from the main process, and when running from an IPython or jupyter notebook interactive kernel, the child's exception and traceback appears to be lost.
A known way to see the child's error, and try to fix or handle it, is to run the problematic code as a batch script from a system's Command Prompt. The child's exception will be printed to the Command Promt's stderr, and it should be visible above this error and traceback.
Note that if running a jupyter notebook that was invoked from a Command Prompt, the child's exception should have been printed to the Command Prompt on which the notebook is running.
調べてみると,下記のサイトが参考になりました.
stackoverflow.com
pm.sampleの引数にcoresを入れるんだとか.coresって何だ?と思ってドキュメントを調べてみたところ,並行して走らせるチェーンの数らしいですね.
docs.pymc.io
最近はnjobsではなく,coresでチェーンの数を設定するんですかね?
そういえば最近,pm.sampleの引数をnjobs=2みたいに指定したら,
ValueError: Unused step method arguments: {'njobs'}
というエラーが出ましたが,これに関係するのかな.公式ドキュメントを見てもnjobsって無いし..
と思って調べたら
下記によれば
njobs have been removed, please use coresinstead
だそうです
github.com
間違えてフォルダを指定すると『PermissionError: [Errno 13] Permission denied』になる
かなり初歩的ですが,1時間位ハマったのでメモ.
teratail.com
たとえば、windowsではフォルダをopenしようとするとそのエラーになります。そういったトラブルがあるのかもしれません。
globの癖とかでフォルダを指定しちゃ駄目なんですよねー
ポアソン分布とガンマ分布から事後分布を導出して,事後期待値や予測分布などを求める
この前までとある所で一般化線形モデルから始まるベイズモデリングの勉強に参加していました.一般化線形モデルを通して勉強したのは初めてかもしれません.ということでベイズモデリングについて体系的に勉強するために記事を書いてみようと思います.
この記事ではまず手始めとしてある例題をもとに,ベイズの定理を用いて事後分布を導出する過程について述べます.
もくじ
こんな例題を考えてみる
この記事では割とよくある例題として,次のような観測値がポアソン分布,事前分布をガンマ分布という場合を考えてみます.
例題
ポアソン分布に従う5つの観測値[2 ,3 ,0 ,4 ,1]が得られたとする.またこのポアソン分布のパラメータはのガンマ分布とする.このとき,
- 事後期待値
- 事後分散
- 予測分布
を求める
得られる標本がポアソン分布に従うものとし,共役な事前分布としてガンマ分布を選んだときに事後分布もガンマ分布になる例を示します.
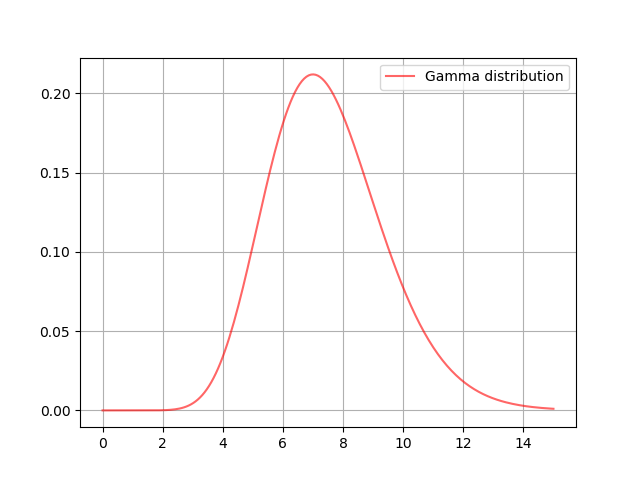
まず事前分布を決める
問題にあるように事前分布としてガンマ分布を考えます.ガンマ分布の密度関数は次のように与えられます.
観測値から尤度関数を求める
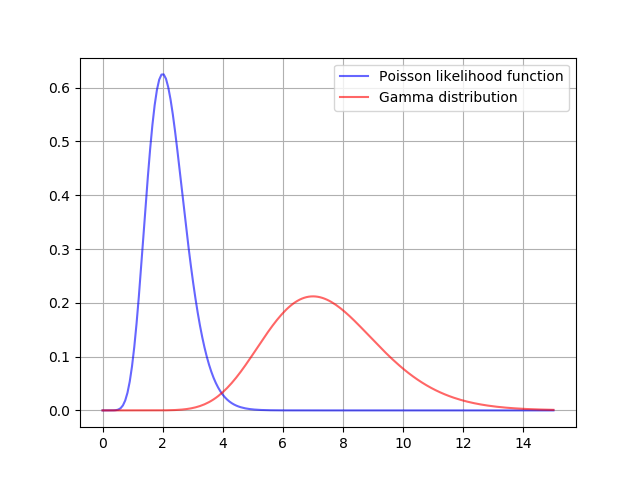
観測値[2 ,3 ,0 ,4 ,1]が与えられた場合は尤度関数は次のように与えられます.
事前分布と尤度関数から事後分布を求める
事後分布は次のようになります.
事前分布と尤度関数と合わせて描画すると次のようになります.観測値をもとに,事前分布が更新されています.

事後分布から事後期待値,事後分散,予測分布をもとめる
事後分布がガンマ分布になることが分かったので,ガンマ分布の期待値と分散の計算より,
予測分布は次のとおりです.
上式について,ガンマ関数の定義より,
参考
- Bayesian Data Analysis 3rd EditionのP44あたり(PDF版がありあす)https://www.amazon.co.jp/Bayesian-Analysis-Chapman-Statistical-Science/dp/1439840954

